<개념>
▶ t-검정
-집단 간 평균 비교를 할 수 있도록 고안된 분석방법
▶ 왜 t-검정을 하는가?
-비교대상과 원대상 간의 차이를 확인하고 그것이 통계적인 의미(수준)에서 차이가 있는지를 살펴보기 위해서 실행
-비교하고자 하는 집단이 2개일 때는 t검정을 하고, 3개 이상일 때난 분산분석(ANOVA)을 한다고 함
▶ 통계적 접근
-비교 집단을 어떻게 볼 것인가에 따라
=> 일표본 t검정(one sample t-test): 모집단의 정보를 알고 있을 때 수집한 표본의 평균과 일치하는지 여부를 확인하는 검정
(예: 표본 집단의 비율 또한 100인지 아닌지 확인할 때 *거의 사용하지 않음)
=> 독립표본 t검정(independent t-test): 독립적인 두 집단의 평균 차이를 비교하기 위한 검정
(예: 상위집단/하위집단, 남자/여자, A집단/B집단 등)
=> 대응표본 t검정(paired t-test): 동일한 대상자를 대상으로 사전/사후 같은 2개의 결과를 비교하기 위한 검정
(예: 사전/사후, 22년/23년 등)
**두 평균값 비교를 통해 가설을 설명하는 방법설명, 반면, 신뢰구간은 측정값(표본에서 구한 모집단 평균값)이 어떤지를 검증하는 추론 통계적방법임
▶ 두 그룹의 평균을 비교하는 방법 3가지
1) t-검정(; t-test, student -test)
- 분석 조건: '결과값이 연속형 변수 - 정규 분포 - 등분산' 인 경우
2) 윌콕슨 순위합 검정(; Wilcoxon rank-sum test)
- 분석 조건: 결과값이 연속형 변수가 아닌 경우, 결과값이 연속형 변수이지만 정규 분포가 아닌 경우
3) 웰치의 검정(; Welch's test)
- 분석 조건: 결과값이 연속형 변수이고 정규 분포를 가지고 있지만 등분산이 아닌 경우
<활용 예제>
▶ Excel을 이용한 (독립표본) t-test 4단계
① 기초 통계량 계산
→ 비교 두 집단 데이터 불러오기
→ 분석도구 - 기술 통계법
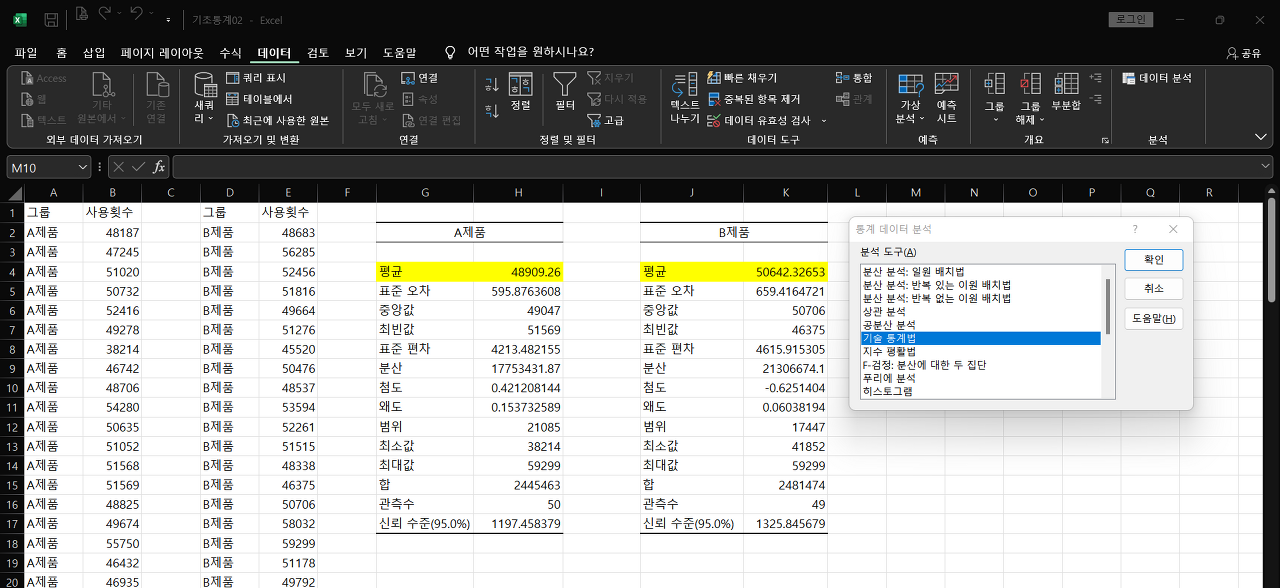
② 등분산 검증
→ 분석도구 - F-검정: 분산에 대한 두 집단
*Tip: P(F<=f) 단측 검정 값이 0.05 보다 크면 두 집단은 차이가 없다 !!
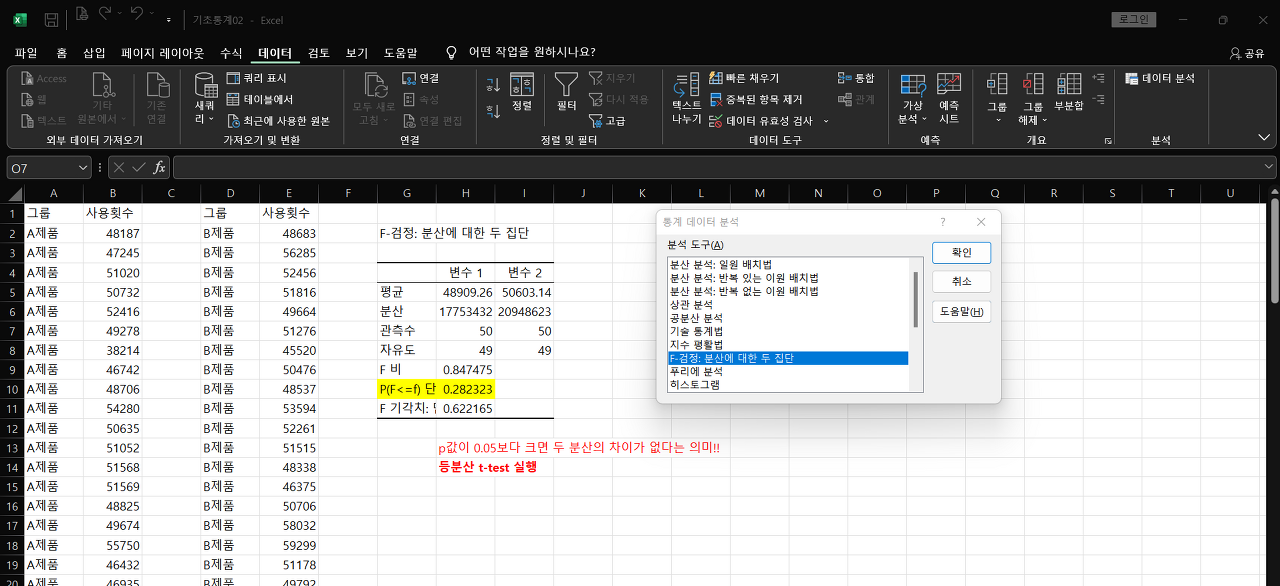
③ 등분산 t-test
→ 분석도구 - t-test: 등분산 가정 두집단
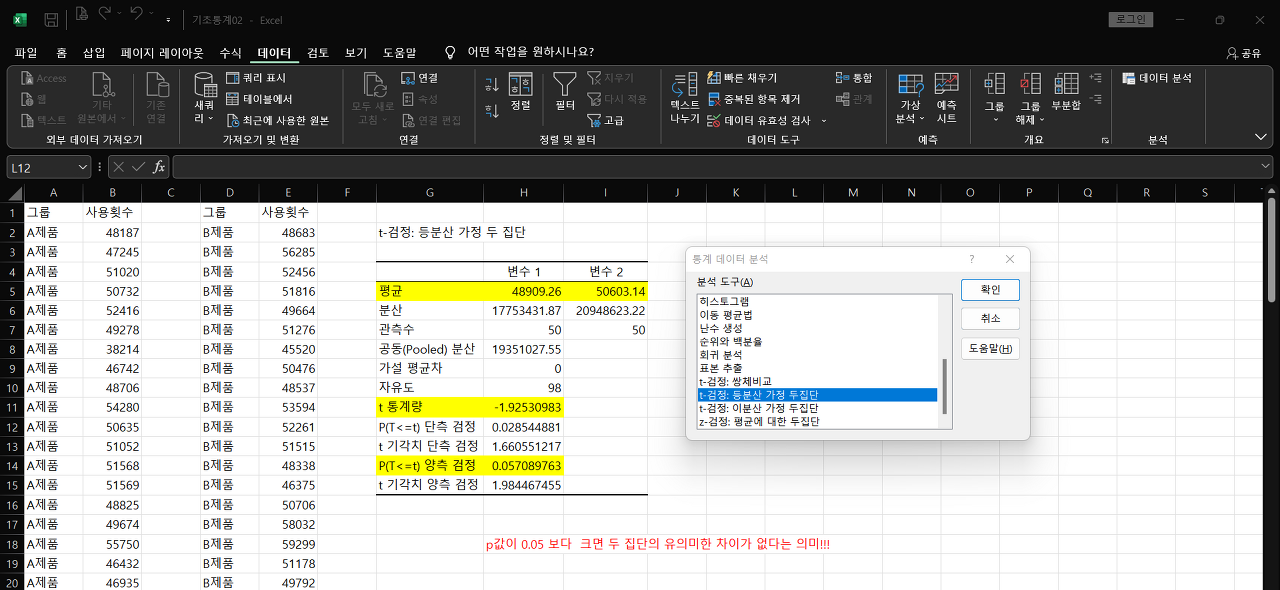
④ 자료 정리 및 시각화
→ 두 집단의 평균값, t-값, p-값 등
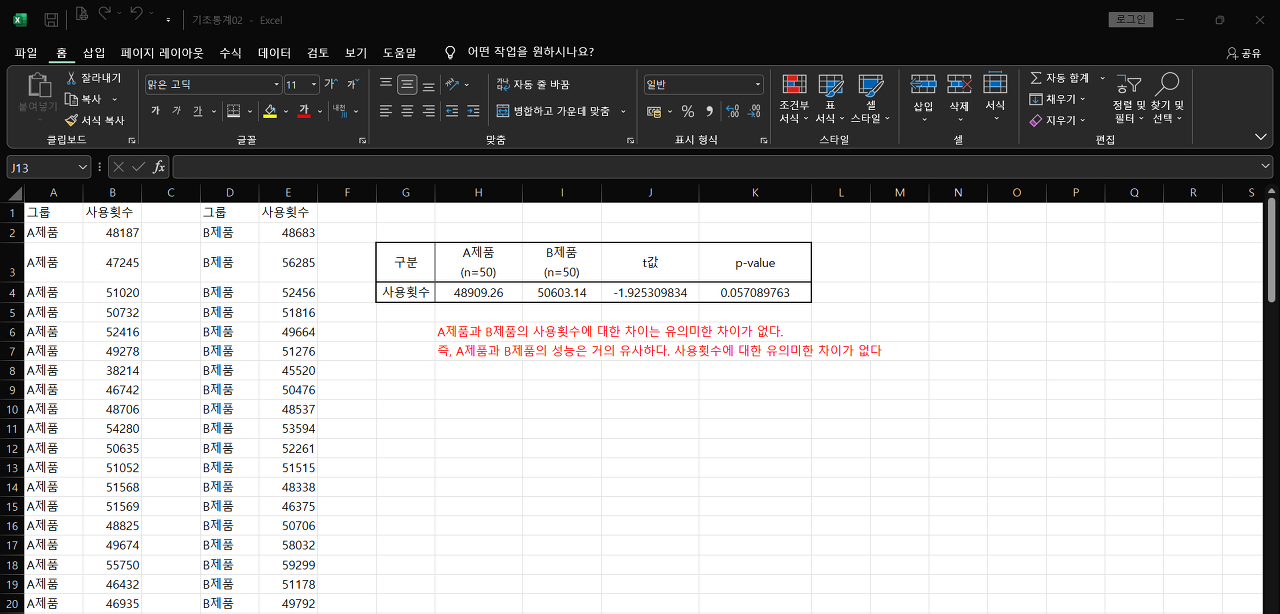
* Excel을 이용한 t-검정 (참고 영상 링크)
석사논문 작성을 위한 기초 통계 6주 완성 - 크몽
용고opt2mot 전문가의 전자책 서비스를 만나보세요. 이런 분들이라면 놓치지 마세요 !!샐러던트: 대학원에서 연구를 시작하는 샐러던트대학원생: ...
kmong.com
------------------ eot
▶가설검정(hypothesis testing)
- 분석자가 세운 가설을 검증하기 위한 방법
- 가설검정에서는 p값(p-value)이라는 수치를 계산하여 가설을 지지하는지 여부를 판단함
▶ p-value(; p값) 란,
귀무가설이(u_a = u_b) 옳다고 가정했을 때 관찰한 값(예: 평균값의 차이) 이상으로 극단적인 값이 나올 확률
=> p값이 작다는 것은 (귀무가설이 옳다는 세계에서는) 현실 데이터가 잘 나타나지 않는다는 뜻
=> 귀무가설과 현실 데이터 간의 괴리 정도를 평가하고 있는 셈
==> 일반적으로 p값이 0.05 이하인 경우, 귀무가설 하에서 현실 데이터는 나타나기 어렵다고 생각하고, 귀무가설을 버리고(; 기각하고) 대립가설(u_a ≠ u_b)을 선택한다(; 채택한다). 이때 평균값의 차이는 "통계적으로 유의미한 차이가 있다(statistically significant)"라고 표현한다.
==> 한편 p값이 0.05를 상회하는 경우 귀무가설을 기각할 수 없으며, "통계적으로 유의미한 차이는 발견하지 못했다"라는 결과가 된다.
*귀무가설을 기각할 것인지 채택할 것안지의 판단 경계로 이용하는 값을 유의수준 a 라고 한다.
*논문 등에서 "통계적으로 유의미한 차이를 발견할 수 없었다(p=0.246)"의 기술에서, 유의미한 차이가 없다는 것은 귀무가설을 지지한다는 것이 아니라, 귀무가설과 대립가설 중 어느쪽도 지지할 수 없어 결론을 보류한다는 판단임을 명심해야 한다.
>> 정규분포 확인하는 방법
* p-값이 0.05 보다 크다면 정규 분포한다고 보면됨, p-값이 0.05 보다 작다면 정규분포를 하지 않는다고 보면됨
예)p=0.004821로 계산 되었다면, p-값이 한참 작으니까 데이터의 정규성(normality)을 가정할 수 없다고 판단함
>> 등분산 확인하는 방법
* p-값이 0.05 보다 크다면 등분산을 한다로 보면됨.
>> t-검정을 하는 방법, 위 두 과정으로 확인한 후,
- 그룹 간의 차이 평균을 비교하여,
- p-값이 0.05 보다 작다면 , 두 그룹의 평균은 통계적으로 의미 있게 차이가 난다라고 볼 수 있다
p-값이 0.05 보다 크다면, 두 그룹간의 평균은 차이가 없다고 해석할 수 있다.
▶ t-값의 의미
- t 값은 표준편차가 얼마나 크고 작냐는 이야기다.
- 표준편차의 절대값은 변수의 단위 등에 따라 상대비교가 불가능하므로, 회귀계수를 표준편차로 나누어 주어서
표준편차의 정도를 상대적으로 비교해 볼수 있게 하는 것이다.
- t 값이 크다는 것은 표준 편차가 작다는 것이다. (독립-종속 변수간 상관도 높음)
*독립변수는 입력값이나 원인을 나타내며(x-축), 종속변수는 결과물이나 효과를 나타낸다.(y-축)
- t 값이 작다는 것은 표준 편차가 크다는 것이다. (관계 낮음)
- 그러므로 유의미한 결과가 나오려면 t 값은 커야 한다.
'Future Strategy > 샐러던트' 카테고리의 다른 글
| 독립성 카이제곱 교차분석 (0) | 2023.09.07 |
|---|---|
| ANOVA 분산분석 (0) | 2023.09.06 |
| 데이터 시각화 (0) | 2023.09.04 |
| 빈도분석 (0) | 2023.09.03 |
| 신뢰도/타당도, 신뢰구간 (1) | 2023.09.02 |




댓글