<개념>
▶ 분산분석(3개 집단 이상의 평균값 비교) : ANOVA(; Analysis of variance)
- 집단 2개 평균비교: t-검정(단, 일표본 t검정은 단일표본에 한함)
- 집단 3개 이상 평균비교: 분산분석
=> 일원배치분산분석(one-way ANOVA) 또는 일변량분산분석
▶ 분산분석의 기본 가정
1) 분포의 정상성 : 모든 집단이 정규 분포여야 한다.
2) 측정의 독립성 : 모든 집단의 측정은 독립적으로 이루어져야 한다.
3) 등간척도 이상의 측정 수준 : 종속변인이 등간척도 또는 비율척도여야 한다.
* 독립 표본 t-검정 때 처럼 등분산 가정 만족하는지 확인 필요.
▶ 분산분석의 종류
- 일원배치 분산분석 (One-way ANOVA) : 독립변인 1개이지만 독립변인을 구성하는 집단이 3개이상인 경우
(예) 학력(초,중,고)에 따른 스마트폰 중독 점수 차이
- 이원배치 분산분석 (Two-way ANOVA) : 독립변인이 2개나 독립변인을 구성하는 집단이 2개 이상인 경우
(예) 성별(남,여) 및 연령(10대,20대) 에 따른 스마트폰 중독 점수 차이
▶ 분산분석의 가설검정 단계
1) 등분산 검정(equal variance test)
2) 분산분석표 유의확률(p) 확인(ANOVA table)
3) 필요시 사후검정(post-hoc test)
▶ 분산분석표(anova table)
- 제곱합(sum sq), 평균제곱(mean sq), F값과 유의확률(p)을 포함하는 통계표이며,
- 분산분석표의 유의확률(p)이 통계적으로 유의하다고 나타나면 회귀방정식(모형)을 사용할 수 있다는 의미가 된다.
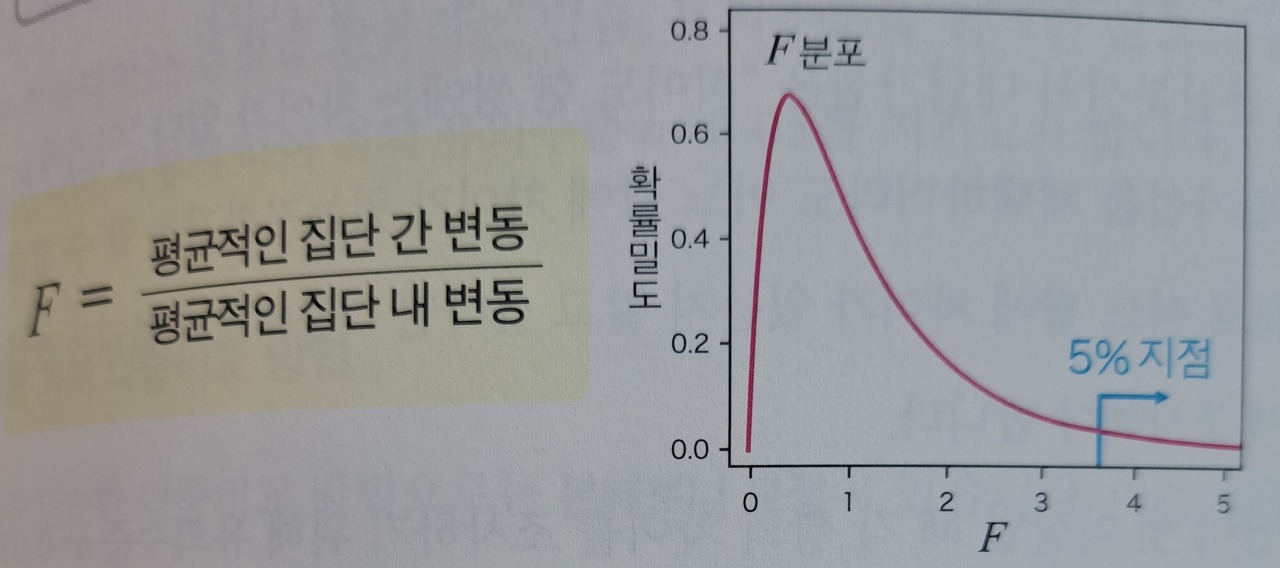
▶ F값=(평균적인 집단 간 변동)/(평균적인 집단 내 평균)
- 관찰한 F값 이상으로 극단적인 값이 나올 확률: p값
*F값이 5% 지점 오른쪽에 있다면 유의수준 a=0.05에서 통계적으로 유의미한 집단 간 차이가 있다는 뜻
- (평균적) 집단 내 변동 ==> 오차에 따른 변동
- (평균적) 집단 간 변동 ==> 효과에 따른 변동
▶ 세 그룹의 평균을 비교하는 방법 3가지
1) ANOVA(; ANalysis Of VAriance)
- 분석 조건: '결과값이 연속형 변수 - 정규 분포 - 등분산' 인 경우
2) 크루스컬-왈리스 H 검정(; Kruskal-Wallis H test)
- 분석 조건: 결과값이 연속형 변수가 아닌 경우, 결과값이 연속형 변수이지만 정규 분포가 아닌 경우
3) 웰치의 ANOVA(; Welch's ANOVA)
- 분석 조건: 결과값이 연속형 변수이고 정규 분포를 가지고 있지만 등분산이 아닌 경우
<활용 예시>
▶ Excel을 이용한 ANOVA(분산분석) 2단계
- 등분산을 가진다는 조건에서,
① 분산분석: 일원배치법
→ 비교 세 집단 데이터 불러오기
→ 분석도구 - 분산분석:일원배치법

② 분산 분석표 정리 및 시각화
→ F비, F-기각치, p-값
* Excel을 이용한 등분산 ANOVA (참고 영상 링크)
※ Excel에서 세 집단에 대한 등분산 검증 (참고 영상 링크)
▶ 사후 검정(; multiple comparision)
- 두 그룹 이상의 평균이 차이가 있는지 없는지를 검정하는 방법(t-test, ANOVA)과 의미를 해석해봤다면,
- 평균이 차이가 있다고 확인되었을 때, 즉, p-값이 유의수준 0.05보다 작게 계산되어 유의미한 차이가 있다고 판단되는 경우, 어떤 그룹과 어떤 그룹의 평균이 차이가 있어서 그런 결과가 나왔는지 알아보기 위해 실시하는 검정
- 세가지 방법이 있음(ANOVA 사후 검정, 크루스칼-왈리스 H 검정 사후 검정, 웰치의 ANOVA 후 사후 검정)
↑ 비교적 간단 ↑ 비모수 검정 ↑ 매우 복잡
석사논문 작성을 위한 기초 통계 6주 완성 - 크몽
용고opt2mot 전문가의 전자책 서비스를 만나보세요. 이런 분들이라면 놓치지 마세요 !!샐러던트: 대학원에서 연구를 시작하는 샐러던트대학원생: ...
kmong.com
'Future Strategy > 샐러던트' 카테고리의 다른 글
| 상관분석-상관관계-상관계수 (0) | 2023.09.08 |
|---|---|
| 독립성 카이제곱 교차분석 (0) | 2023.09.07 |
| 엑셀을 이용한 t-검정 (0) | 2023.09.05 |
| 데이터 시각화 (0) | 2023.09.04 |
| 빈도분석 (0) | 2023.09.03 |




댓글