<개요>
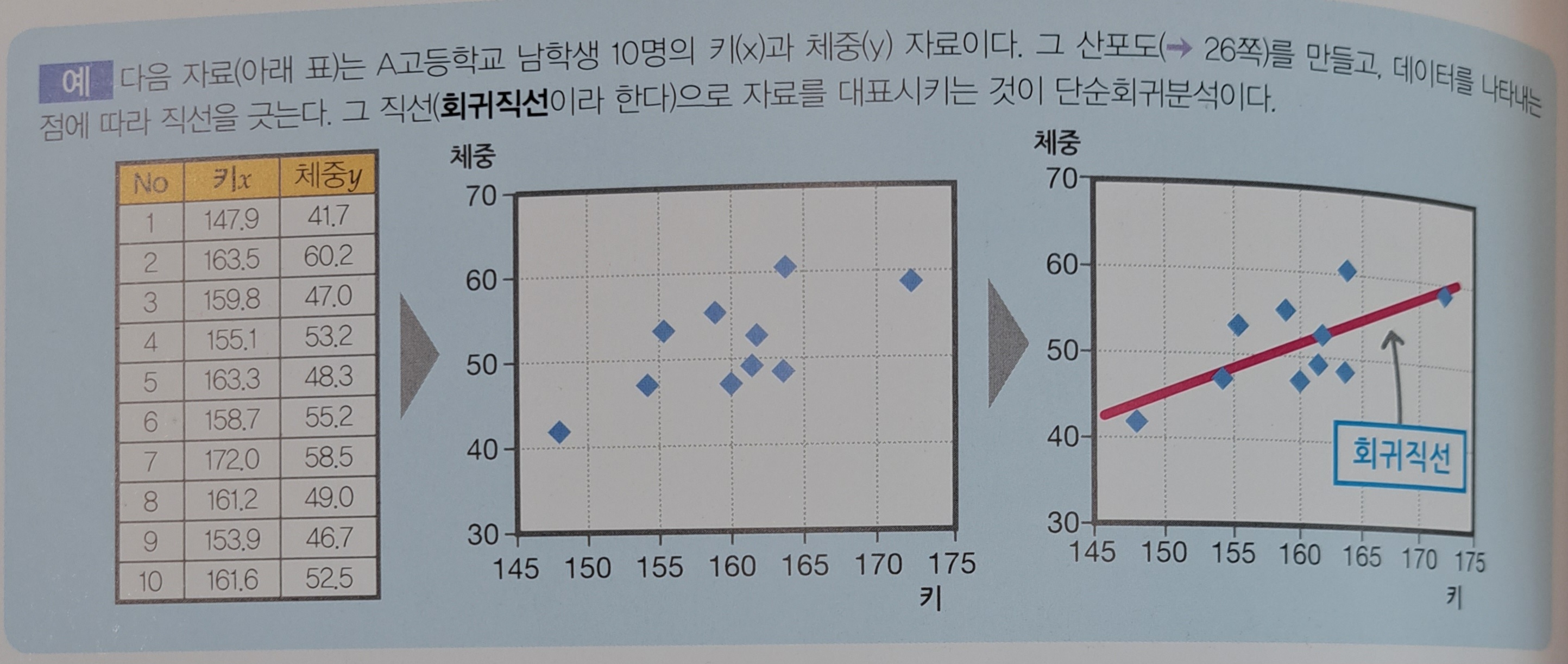
▶단순회귀 분석
- 2변량의 관계를 수식으로 나타낸 것. 보통 선형 단순 회귀 분석이 많이 사용된다.
- 선형회귀분석이 요구되는 통계적 가정들은 분석 후 결과 해석에 대한 객관성을 보장해주는 역할을 한다.
* 분산분석표(anova table)는 제곱합(sum sq), 평균제곱(mean sq), F값과 유의확률(p)을 포함하는 통계표이며, 분산분석표의 유의확률(p)이 통계적으로 유의하다고 나타나면 회귀방정식(모형)을 사용할 수 있다는 의미가 된다.
<활용 예제>
▶ Excel을 이용한 단순회귀분석 3단계
ⓛ 상관 분석
→ 비교 집단(종속 변수) 데이터 불러오기
→ 분석도구 - 상관 분석

② 단순회귀분석
→ 분석도구 - 회귀 분석

③ 회귀 방정식(; 회귀직선) 해석하기
→ 결과 해석 : 결정계수 (; R^2), 표준 오차, F-비(; F-통계량), 유의한 F(; significance F, F-통계량에 상응하는 p-값)
※ 일반적으로 0.05 보다 작다면 독립변수와 종속변수간에는 유의미한 상관관계가 있다.
→ 회귀분석 시각화: 산점도, 추세선, 회귀방정식 등


* Excel을 이용한 단순회귀분석 (참고 영상 링크)
석사논문 작성을 위한 기초 통계 6주 완성 - 크몽
용고opt2mot 전문가의 전자책 서비스를 만나보세요. 이런 분들이라면 놓치지 마세요 !!샐러던트: 대학원에서 연구를 시작하는 샐러던트대학원생: ...
kmong.com
----------------------------------- eof
단순 회귀 분석
*상관계수를 제곱한 값
>> 하나의 요인으로 현상을 설명하기
>> 다음 관찰값들이 어떻게 관찰될지에 대한 예측
- 하나의 독립변수로 또 다른 종속 변수(결과 변수)를 예측하는 것 => 단순 선형 회귀 분석
** 대개 우리의 연구는 관심을 두는 종속 변수(결과값)가 하나의 독립 변수로 충분히 설명되는 경우는 거의 없음!!
>> 즉, 대개 적게는 서너개 또는 그 이상의 독립변수들을 고려해야 종속 변수가 그나마 예측되는 경우가 많음
>> 다중 회귀 분석
- 1) 상관계수 계산시 0.99549... 로 계산된 경우 ==> 상관성이 매우 크다고 판단
- 2) 상관 계수를 제곱한 실행력이 0.999100... 이 됨 ==> 이 경우 독립변수와 종속변수는 서로를 99.1%나 설명한다고 알 수 있음
- 3) 관찰한 값을 표시 하는 좌표들과 이 사이를 지나는 직선과의 수직적 길이를 가장 짧게 하는 최소 제곱법을 이용해 선형 모형을 만들수 있음 ==> <메디컬 빅 데이터 연구를 위한 R 통계의 정석(김종엽 저) p190
- 선형 회귀 모형(회귀식의 함수/그래프)을 구했다고 끝?? ==>( 아님 )
==> <메디컬 빅 데이터 연구를 위한 R 통계의 정석(김종엽 저) 13강
- 4) 최소 제곱법으로 추정한 선형 회귀 모형을 수용하기 위한 기본 가정 4가지를 만족해야 함
>> 1. 정규성(normality) => Normal Q-Q <= 정규성 확인을 위한 그래프
>> 2. 선형성(linearity) => Residuals vs. Fitted <= 선형성을 확인하기위한 예측값에 따른 잔차의 분포 그래프
>> 3. 독립성(independence) => Scale - Location <= 예측값에 대한 표준 편차 그래프
>> 4. 등분산성(homoscedasticity) => Residuals vs. Leverage <= 영향력이 큰 관찰값들에 대한 그래프
'Future Strategy > 샐러던트' 카테고리의 다른 글
| 다중회귀분석 (0) | 2023.09.10 |
|---|---|
| 상관분석-상관관계-상관계수 (0) | 2023.09.08 |
| 독립성 카이제곱 교차분석 (0) | 2023.09.07 |
| ANOVA 분산분석 (0) | 2023.09.06 |
| 엑셀을 이용한 t-검정 (0) | 2023.09.05 |




댓글